 Photo taken from Weebly.com gallery of photos Bees are one of the best known pollinators in the botanical world. The sweetness of Nature relies on the art of symmetry of the relationship between flower and the Bee. The result is the collection of sweet, luscious, nectar. Once all the nectar has been dutifully collected, the bee comes back to the hive, where the nectar will turn into nourishment for her and the rest of the colony. What is fascinating is shape of the hive she is in, the storage bins for the nectar. Bees are also one of the best geometers. So why are the honey comb cells hexagonal? Well, it is time to be a kid and blow some bubbles first.  Photo taken from Weebly.com gallery of photos The bubble, or the sphere, is the most efficient shape to hold what is inside, a given volume. It is the perfect relationship of surface area to volume. Individually, the spheres can exist in maintaining this ratio without distortion. However, if you go get a glass of milk and a reusable straw, you will find that competition for a given area will change the geometry of this perfect ratio. In other words, the geometry of the bubble will change. The story of milk and bubbles actually began, for me, about five years ago when writing a math blog about lessons to do at home with children. There is nothing more fun than to get a glass of milk, a straw, and blow bubbles. While you are having some fun, you could also notice how the spherical bubbles would get bigger and bigger and then quickly form other little bubbles to fill the gaps, in between the bigger ones. Then, as more and more seemed to be created, those wonderful spherically shaped bubbles would then form into something hexagonal in shape (link to "Math on the Mountain: The Geometry of Streams, Bubbles, and Chocolate Milk"). The same happens to a moving stream of water, along the desert wash. As more and more bubbles form, they are doing their best in aerial/water tiling, as they press against the other. Tiling happens in Nature when shapes are trying to fit into the most efficient pattern that will result in having less spaces/gaps in between the next shape. Sometimes that results in little tiny bubbles fitting into the spaces, and sometimes those bubbles will take on a hexagonal form to them, just like what happens to the bee hive "storage bins" for their nectar.  Learning Math with Mom Copyright All Rights Reserved  Learning Math with Mom Copyright All Rights Reserved In tiling, one of the shapes that can be used individually over and over again, are hexagons, not spheres. Over thousands of years and many generations, Bees have used this six-sided polygon, the next best thing to spheres and maintaining that ratio, to be the most efficient way to store their hard earned harvested nectar, to provide a food source for the rest of their colony. Symmetry, geometry, finding that perfect ratio, it is all there. It is there in Nature.
Many Blessings References: Cornell University (May 2004). Bubbles! http://pi.math.cornell.edu/~mec/2003-2004/geometry/bubbles/bubbles.html Grossman, C. (2016). Math on the Mountain: The Geometry of Streams, Bubbles, and Chocolate Milk. https://learningmathwithmom.wordpress.com/2016/09/01/math-on-the-mountain-the-geometry-of-streams-bubbles-and-chocolate-milk/ Illustrative Mathematics (2016). Hexagonal Pattern of Beehives. https://tasks.illustrativemathematics.org/content-standards/tasks/1126
0 Comments
 German Chamomile, also known as Matricaria recutita, is a part of the Aster family (Asteraceae). The way I grew up knowing her was by calling her Manzanilla, the little apple. Why? Because she was often described as her flower smelling like an apple, or the tea tasting like a green apple. But what causes this flower to have the scent and smell of an apple?
Upon studying the components of German Chamomile for a case study, my goal was to look for the therapeutic properties of the essential oil. What I found was that one of the components of this magnificent flower is trans-B-farnesene. Although I could not find the therapeutic properties connected to this acyclic sesquiterpene alkene, this component serves a different olfactory purpose. What was interesting is that trans-B-farnesene is also found in green apple and the scent of green apple. The green apple and German Chamomile have the same scent because of trans-B-farnesene! Sometimes, looking up components for their therapeutic properties may lead you to not finding one, but leading you to the connection she has to another fruit of a plant, like green apple. I love Nature, don’t you? Many Blessings Resources: Ethan B. Russo, Jahan Marcu, in Advances in Pharmacology, 2017 https://www.sciencedirect.com/topics/pharmacology-toxicology-and-pharmaceutical-science/beta-farnesene  Calendula officinalis & Bee in Arizona 2021 Symmetry is something that we have some basis of understanding of what that is. We may often see Symmetry in its geometric application on pieces of paper demanding for us to search for symmetry of a given object. But why? What application could this possibly have apart from this two-dimensional space? We possibly could extend our thinking of symmetry as balance, or something that is the same on both sides. When we walk out of our homes and offices, we could surely go out and observe in even the three-dimensional space, but how does this relate to a language of Nature that is often discussed over and over again?
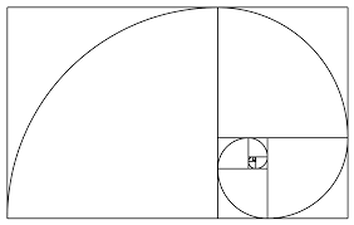
One sense of the word, according to Wikipedia, is that it is an “agreement of dimensions, due proportion, and arrangement”. It was profound to see the words agreement of dimension. This definition resonated with me as it relates back to this language in Nature about an agreement of how things are created, an agreement of how they thrive, and an agreement with how they transition onto the next generation and season. In Nature, we may often feel and think that to thrive is to compete in order to survive. For most things, proportion and arrangement is agreed upon in order to maintain a balanced ecosystem for life. In all these things and in all that time and space in between those defining moments of life, is also a beautifully intricate art form of pollination and growth. When thinking about Symmetry, it is an art form that is agreed upon, but not necessarily always a competition, but an arrangement of understanding. In that result, the art form thus produces the sweetness of life. Let us consider the bee, for example, as the pollinator. It has taken thousands of generations of bees, more than that of course, to come up with the wisdom to decide which plants and trees to pollinate. As that transpired, there were subtle forms of communication transforming with the rest of the botanical world. The result of that communication was an evolved arrangement of stigma, stamen, pistil, and petals, all in balance and all in symmetry. The symmetry of this arrangement is extremely important as, according to Du Sautoy, “…provides a way of animals (bees) and plants to convey a multitude of messages, from genetic superiority to nutritional information” (pg. 11). Think of this as its own art form. This presentation is more than just something beautiful to look at, but a form of a Mathematical language that is communicated between pollinator and plant. Why? Because those flowers who are symmetrical, produce the sweetest culinary experience for the bee. “Symmetry tastes sweet” (Sautoy, pg. 12). Over an extensive period of time, Symmetry as proved itself to be part of the sweetness and art of pollination. Many Blessings References: Du Sautoy, M. (2008). Symmetry. (pgs. 11-12). Harper Collins Publishers. Wikipedia. (2021, February 13). Symmetry. Retrieved from https://en.wikipedia.org/wiki/Symmetry#cite_note-1  During my undergraduate studies, there was a Mathematics class where we had the discussion of whether Mathematics was a human invention, or if it was already created in the Universe. There are those of us who may fall into one category, or the other. There are also those who are in-between. What I hope cannot be disputed, emphasis on hope, is that the behavior of patterns was in practice before we existed. In describing this behavior, the written and documented application came forth as a universal language that is called Mathematics. Whether we speak a different spoken language, or come from a different part of the world, we both can speak and apply Mathematics because it is a language we can both understand, without things being lost in translation. Having said this, for Physics and Quantum Physics, I completely understand if you do not agree with me here if you feel Mathematics may have limitations, but so does everything else. Context just may be the birthplace of applying limitations. In all things, it is a language that applies to describe the behavior of the Universe in terms of numbers, patterns, and geometries, regardless of where we call home. In my philosophy, the behavior of patterns was already in existence. I could not imagine a human being teaching a bee, for example, on effective methods of building hexagonal shaped compartments within the hive for better storage. These were practices over a span of time, passed down from generation to generation, that bees have understood for their own survival and wellbeing. The same can be understood botanically. Botanically speaking, plants have learned and adapted over time on which patterns and geometries produce the best results of being pollinated, creating the best nectar, for thriving growth, and reproduction under changing conditions, or within their sustained environment. Both animal kingdom and plant kingdom practice this dance of patterns, if you will, that is this intelligent composed music of the Universe. What we have done is write down the notes, played it to listen for our own understanding and experience, and painted the picture using the language of Mathematics. In order to continue to dance in harmony and melody, we continue to observe, continue to learn from our Botanical teachers, and protect what was already thriving, before we existed, so that this can continue in existence for generations to come. Many Blessings  Helianthus spp. in Arizona 2021 The Sunflower is part of the Helianthus genus and the Asteraceae family. Sunflowers are very accessible, both in cities and in rural areas of North America. If you have ever grown your own Sunflowers, purchased them at the grocery store, or picked them from the farm, you may understand when I say how they spread joy and happiness to those around them. They brighten the area like the Sun. The Sunflowers, via stretching their stems, actually do follow the path of the Sun. The path of following the Sun from East to West is called rhythmic tracking and allows for optimal growth for the Sunflower (Crespi, 2016). There have been further studies on Sunflowers who face East versus West. Those facing East have increased visits from pollinators, such as bees, during the daytime. The increase is so profound, that it is five times more than those not facing the same direction (Crespi, 2016). At the very center of the Sunflower, there are also two spiraling systems that begin from the center. With what we know about symmetrical growth in Nature, one would assume that the spiraling effect in Sunflowers also follows the same rule, but it does not. The number of spirals from the center, that are both clockwise and counterclockwise, are not equal in number. The ones who did have the time to count the number of clockwise and counterclockwise spirals noted that those numbers are true to showing the pattern of successive Fibonacci numbers. “The number of spirals in two directions may be 21 and 34, or they may be 8 and 13” (Hemenway, 2005). Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ... What is fascinating is that our Sunflowers- Helianthus spp. follow this Mathematical system of numbers in the Fibonacci sequence and also follow a rhythmic system. These are patterns that are part of their health, their wellbeing. Before you venture out into the garden, the grocery store, or to the local farm, think about observing like a Mathematician, or Scientist. Think about growing your own Sunflowers at home. Make observations and find more stories that Helianthus spp. wants to share on how to live in the patterns of Mathematics in Nature. Many Blessings References: Heatherley, A. (1998). Healing Plants: A Medicinal Guide to Native North American Plants and Herbs. (pgs. 211-212). The Lyons Press. Hemenway, Priya. (2005). Divine Proportion: Phi in Art, Nature, and Science. (pg. 137). 1st edition. Sterling Publishers. Crespi, S. (April 2016) Science Magazine: Why Young Flowers Follow the Sun. https://www.sciencemag.org/news/2016/08/why-young-sunflowers-follow-sun  Ponderosa Pine Needle Cluster Mount Lemmon, Arizona 2020
Fibonacci, an Italian Mathematician, was not the first person to discover the number patterns in Nature, but he was most likely the first to publish the information and have his documentation accepted (Just putting this out here). What was documented were patterns in Nature, in the growth patterns of animal populations, or even in the number of petals of a flower to the Pine needles in a cluster.
|
AuthorI am not the first, nor the last of expressing and sharing the beauty of mathematics in Nature. What I will share in this blog are thoughts, experiences, and lessons learned to validate life, both human and botanical, living mathematically. Archives
September 2021
Categories
All
|
RSS Feed
